Harnessing Language Models for Smarter Optimization

Using Language Model Crossover to replace hand‑crafted operators and unlock scalable, domain‑agnostic optimization across diverse problem spaces 

Language models have revolutionized computational problem-solving, excelling in applications like text generation, programming, and data synthesis. Yet their potential remains underexplored in many areas, particularly in optimization, where they could transform how we generate and refine solutions. These models are not just tools for interpreting language; they are adaptable pattern-recognition engines capable of driving innovation across disciplines.

Evolutionary algorithms are a powerful approach to optimization, but they often rely on carefully engineered operators to generate new solutions — a process that demands significant domain expertise and limits broader application. This raises a critical question: could language models be repurposed to eliminate this bottleneck, streamlining the process while amplifying its effectiveness?

In our recent paper published in TELO, we introduce the concept of Language Model Crossover (LMX), a novel method that harnesses the generative power of language models within evolutionary algorithms. By treating these models as flexible operators for solution generation, LMX offers a highly general, scalable approach to optimization, paving the way for broader accessibility and new breakthroughs in problem-solving.

Rethinking optimization with Language Model Crossover

Modern evolutionary algorithms often rely on hand-designed genetic operators tailored to specific domains. While effective, these operators frequently require significant domain expertise and labor-intensive customization, making it challenging to scale their application across diverse problem spaces. Moreover, traditional operators like mutation and crossover often struggle to generate semantically meaningful variations in complex or unstructured domains such as natural language, mathematical expressions, or code. This bottleneck highlights the need for a more adaptable approach to recombination, capable of handling the growing complexity and diversity of optimization tasks.

Language Model Crossover (LMX) emerges as a compelling solution to this challenge. By leveraging large language models (LLMs), LMX transforms the problem of designing domain-specific operators into a generalizable process of using few-shot prompting. This approach allows LMX to recombine text-based genotypes — such as code, equations, and natural language — into high-quality offspring with minimal domain-specific tuning. Through its inherent adaptability, LMX enables evolutionary algorithms to scale across domains with unprecedented ease.

How LMX works

LMX functions as a recombination operator in evolutionary algorithms, using LLMs to generate new solutions. Few-shot prompting works because the language model can “guess the pattern” behind a few input/output pairs and generalize its behavior to a new target input. This ability enables LMX to serve as intelligent evolutionary crossover, creating offspring that incorporate meaningful recombinations of parent traits.

To illustrate how LMX works, we’ll demonstrate it with binary strings — simple text representations composed of 1s and 0s. The goal is to evolve these strings to solve the OneMax problem, a classic optimization task where fitness is determined by the total number of 1s in a string.

Parent selection and input preparation

The process begins by selecting high-performing individuals (parents) from the current population based on their fitness scores. With the goal of maximizing the number of 1s in an 8-bit string, two strong candidates might be selected: 11101111 and 11110111.

Offspring generation and validation

LMX then combines these binary strings to produce new candidate solutions. Multiple parents — e.g., “11101111”, “11110111”, and “10100111” — are merged into a prompt for the language model. The LLM processes this input and generates offspring such as “11111111” or “10110111”. These offspring reflect recombinations of patterns from the parent strings while introducing novel variations.

Population update and iteration

In the final stage, offspring are evaluated based on their fitness — the number of 1s in each string. For instance, “11111111” (fitness 8) would outperform “10110111” (fitness 6). The highest-performing offspring are retained for the next generation, while lower-fitness solutions are discarded. Repeating these recombination and selection steps drives the population toward the optimal solution of all 1s. Over successive generations, the population converges on solutions with higher numbers of 1s, reflecting the optimization process driving toward the OneMax objective.

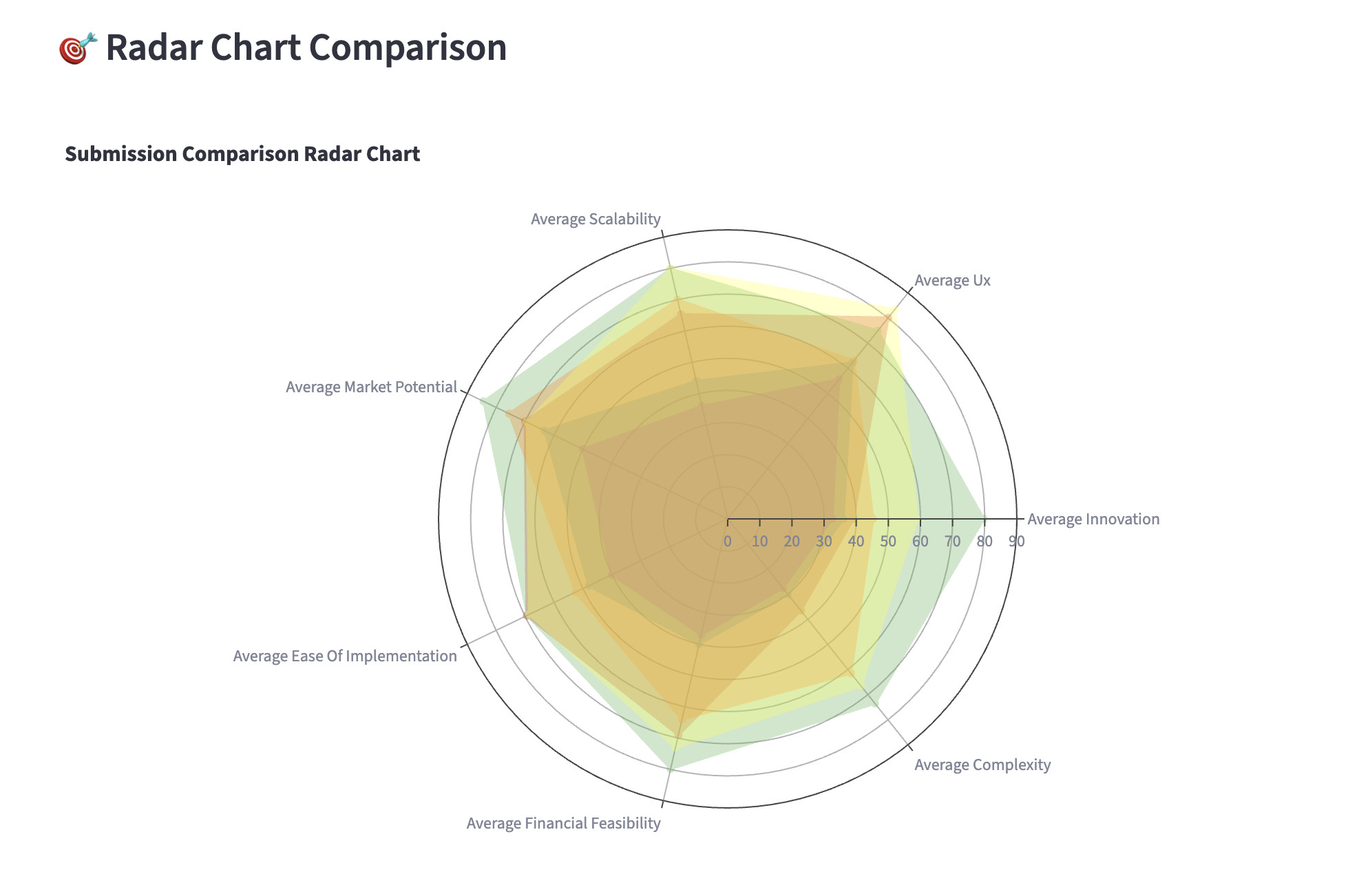
Figure 1 demonstrates LMX’s effectiveness in evolving binary strings. Figure 1a highlights heritability, showing that offspring generated from high-fitness parents retain traits (e.g., a high number of 1s). Figure 1b illustrates population convergence, where fitness values improve over generations, ultimately solving the OneMax problem.

Real world impact of LMX

While binary strings demonstrate the mechanics of LMX, the method’s true strength lies in its broad applicability across domains. In symbolic regression, LMX evolves mathematical expressions, leveraging off-the-shelf scientific language models like GALACTICA to uncover compact and interpretable equations. This eliminates the need for hand-crafted operators in solving data-driven problems.

In creative and technical fields, LMX optimizes text-to-image prompts for models like Stable Diffusion, refining visual outputs such as color or style. Additionally, LMX evolves Python programs in environments like Sodaracers, showcasing its utility in automating code generation and optimization. By seamlessly integrating with domain-specific tools and datasets, LMX serves as a flexible optimization engine, extending the reach of evolutionary algorithms to diverse, text-representable tasks.

Read the full paper.