Unlocking Scalable LLM-Agent Systems with Asymptotic Analysis

Rethinking decomposition, efficiency, and architecture for the age of agentic AI with AALPs research method 

Large Language Model agents are quickly becoming central to AI applications, from automating research to improving software development. As these systems grow in complexity, the natural instinct has been to design them like human teams — breaking down tasks into specialized roles and assigning agents accordingly. Is this the most efficient way to scale LLM-based systems?

At small scales, intuitive decomposition methods may seem effective, but when applied to larger, more complex problems, they often introduce inefficiencies that limit scalability. This paper argues that if we want to build LLM-agent systems that scale to millions of users and tasks, we cannot rely on intuition alone. Instead, we need asymptotic analysis with LLM primitives (AALPs) — a framework for understanding the fundamental computational costs of agent-based AI. By treating each LLM forward pass as the atomic unit of computation (an “LLM primitive”), we can analyze how different architectures scale over time — providing a formal way to reason about efficiency at scale.

In this blog, we explore why asymptotic analysis is critical for scalable LLM-agent systems, identify inefficiencies in current multi-agent designs, and present key insights for building more efficient AI architectures.

The Challenge: Efficiently Scaling LLM Agent Systems

The promise of LLM agents lies in their ability to decompose large problems into smaller, specialized tasks, enabling more efficient solutions. However, as these systems scale to millions of users and increasingly complex tasks, we face a fundamental efficiency problem:

• How should tasks be optimally distributed across LLM agents to minimize computational cost?
• What is the asymptotic behavior of LLM-agent systems as the number of agents and problem complexity grow?
• How can we design systems where each LLM agent contributes efficiently without unnecessary overhead?

Current approaches to LLM agent orchestration are largely intuitive — they reflect how humans might organize work, rather than what is provably efficient. Without a formal framework for analyzing these systems, we risk building LLM-based architectures that function well at small scales but break down as complexity grows.

Our research introduces asymptotic analysis with LLM primitives (AALPs) as a way to rigorously evaluate LLM-agent efficiency. By modeling computational cost based on the number of LLM calls (primitives) rather than treating each agent as a monolithic entity, we gain insight into how these systems behave under extreme scaling conditions.

Optimizing problem decomposition with AALPs

A key application of AALPs is understanding how LLM-based agents should be structured to achieve optimal efficiency. We examined different multi-agent decompositions and found that naive approaches can lead to exponential inefficiencies at scale.

For example, consider a k-task routing problem, where a system must process multiple types of requests. A naive approach might use a single generalist LLM agent capable of handling all tasks, incurring a high computational cost per request. In contrast, an optimized delegator-specialist model uses a delegator LLM to route tasks to much smaller highly specialized LLMs. This approach scales better, with computational savings growing as the number of task types increases.

Similarly, we examined LLM-based code debugging and found that intuitive multi-agent solutions — where a QA agent repeatedly reviews large codebases and a debugging agent rewrites entire sections — incur quadratic inefficiencies. Instead, a more focused decomposition, where the QA agent reviews only specific functions and the debugging agent operates locally, can dramatically reduce computational overhead.

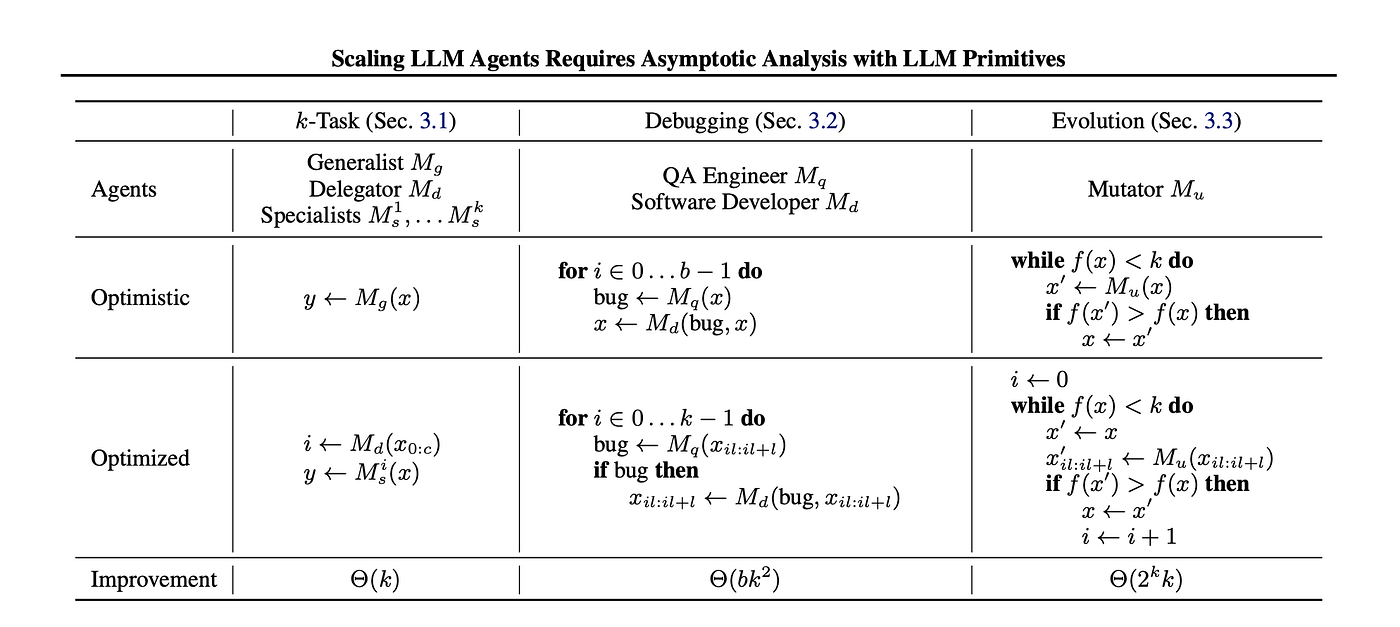
This table gives a high-level summary of the examples described. It lists the LLM agents used, and gives pseudocode for the optimistic implementation (i.e., based on an intuitive belief in the power of LLMs) and the optimized one (based on a more careful LbA design). The improvements result from applying AALPs to these implementations.

Asymptotic analysis in LLM-based optimization

Beyond task decomposition, AALPs also provide insights into how LLM agents should be used for optimization problems, such as code generation, design tasks, and decision-making.

In LLM-driven evolutionary optimization, a common approach is to generate multiple candidate solutions and iteratively refine them. A naive global mutation strategy — where an LLM modifies an entire solution at once — quickly becomes computationally infeasible due to exponential growth in the search space. Instead, a local mutation approach, where an LLM refines specific solution components sequentially, can lead to super-exponential efficiency gains.

Our analysis highlights the importance of precision decomposition — breaking down LLM computations into the smallest possible atomic units — to achieve scalability in optimization tasks.

Looking forward

As LLM-based systems continue to grow, AALPs provides a crucial framework for ensuring their efficiency at scale. Our research highlights several key takeaways:

• Problem decomposition is critical: Careful decomposition of tasks among LLM agents leads to dramatic efficiency gains, preventing systems from becoming computationally infeasible.
• LLM selection matters: Smaller, specialized LLMs should handle discrete tasks, while larger models should only be used where necessary.
• Optimization requires asymptotic thinking: Many current multi-agent approaches are intuitive but inefficient at scale — AALPs provide a formal way to identify optimal strategies.

Beyond efficiency, AALPs also offers broader implications for interpretable, auditable, and ethically aligned AI systems. By designing modular, decomposable architectures, we move toward LLM-agent systems that are not only scalable but also more transparent and adaptable.

For a deeper dive into our findings, read the full paper.